ctidh.h File Reference

#include "../common/namespace.h"
#include "../common/fp/mulx/fp.h"
#include "../common/mont.h"
#include "../common/primes.h"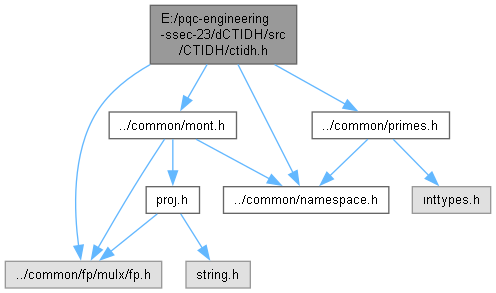

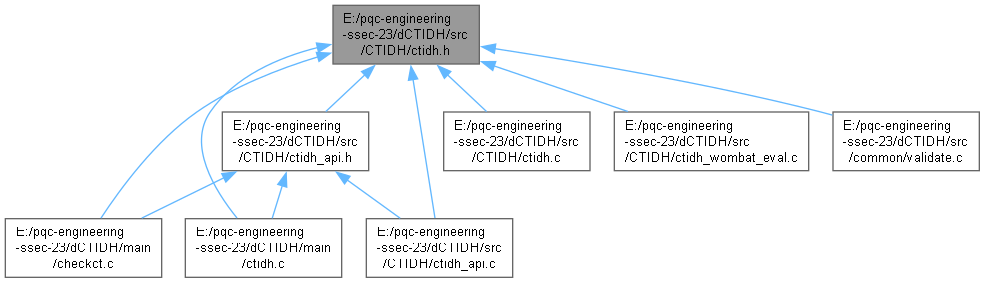
Include dependency graph for ctidh.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Data Structures
struct	private_key
struct	public_key

Macros
#define	csidh_stattried   NS(csidh_stattried)
#define	csidh_statsucceeded   NS(csidh_statsucceeded)
#define	base   NS(base)
#define	ctidh_private   NS(ctidh_private)
#define	csidh   NS(csidh)
#define	validate_cutofforder_v2   NS(validate_cutofforder_v2)
#define	validate   NS(validate)
#define	action   NS(action)
#define	cofactor_multiples   NS(cofactor_multiples)
#define	get_full_point   NS(get_full_point)
#define	fulltorsion_points   NS(fulltorsion_points)
#define	validate2   NS(validate2)

Typedefs
typedef struct private_key	private_key
typedef struct public_key	public_key

Functions
void	ctidh_private (private_key *priv)
bool	csidh (public_key *out, public_key const *in, private_key const *priv)
bool	validate (public_key const *in)
void	action (public_key *out, public_key const *in, private_key const *priv)
void	cofactor_multiples (proj P[], proj const A, size_t lower, size_t upper)
uint64_t	get_full_point (proj *P, proj *A)
void	fulltorsion_points (fp u, fp const a)

Variables
long long	csidh_stattried [primes_batches]
long long	csidh_statsucceeded [primes_batches]
const public_key	base

Macro Definition Documentation

action

#define action   NS(action)

Definition at line 54 of file ctidh.h.

base

#define base   NS(base)

Definition at line 44 of file ctidh.h.

cofactor_multiples

#define cofactor_multiples   NS(cofactor_multiples)

Definition at line 55 of file ctidh.h.

csidh

#define csidh   NS(csidh)

Definition at line 51 of file ctidh.h.

csidh_statsucceeded

#define csidh_statsucceeded   NS(csidh_statsucceeded)

Definition at line 23 of file ctidh.h.

csidh_stattried

#define csidh_stattried   NS(csidh_stattried)

Definition at line 21 of file ctidh.h.

ctidh_private

#define ctidh_private   NS(ctidh_private)

Definition at line 47 of file ctidh.h.

fulltorsion_points

#define fulltorsion_points   NS(fulltorsion_points)

Definition at line 57 of file ctidh.h.

get_full_point

#define get_full_point   NS(get_full_point)

Definition at line 56 of file ctidh.h.

validate

#define validate   NS(validate)

Definition at line 53 of file ctidh.h.

validate2

#define validate2   NS(validate2)

Definition at line 58 of file ctidh.h.

validate_cutofforder_v2

#define validate_cutofforder_v2   NS(validate_cutofforder_v2)

Definition at line 52 of file ctidh.h.

Typedef Documentation

private_key

typedef struct private_key private_key

public_key

typedef struct public_key public_key

Function Documentation

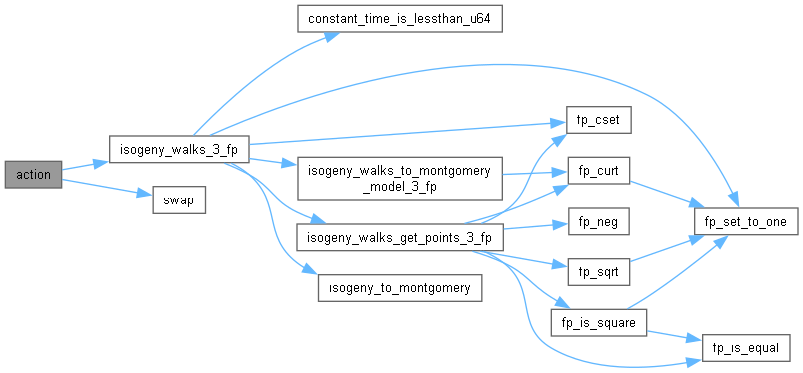
action()

void action	(	public_key *	out,
		public_key const *	in,
		private_key const *	priv
	)

Definition at line 176 of file ctidh.c.

{
// #if !defined(_M1_) && !defined(_M2_) && !defined(_M3_) && !defined(_M4_) && !defined(_M5_)
//   printf("\nNOT using radical 3-isogenies (action).\n\n");
// #else
//   printf("\nUsing 2^%ld radical 3-isogenies.\n\n", batch_start[0] - 1);
// #endif
 
  init_counters();
 
  proj A;
  fp_copy(A.x, in->A);
  fp_copy(A.z, fp_1);
 
  proj A24;
  xA24(&A24, &A);
 
  proj Points[2];
  fp seed;
  fp_set(seed, in->seed);
  fp_enc(seed, seed);
  elligator_seeded(&Points[0], &Points[1], &A24, (const fp *)seed);
 
  clearpublicprimes(&Points[0], &A24);
  clearpublicprimes(&Points[1], &A24);
 
  // clear ells replaced by radical 3-isogenies
  for (int16_t j = 0; j < batch_start[0]; j++)
  {
      xMUL_dac(&Points[0], &A24, 0, &Points[0], primes_dac[j], primes_daclen[j], primes_daclen[j]);
      xMUL_dac(&Points[1], &A24, 0, &Points[1], primes_dac[j], primes_daclen[j], primes_daclen[j]);
  }
  // clear ells not used in the keyspace
  for (int16_t j = batch_stop[primes_batches - 1] + 1; j < primes_num; j++)
  {
    xMUL_dac(&Points[0], &A24, 0, &Points[0], primes_dac[j], primes_daclen[j], primes_daclen[j]);
    xMUL_dac(&Points[1], &A24, 0, &Points[1], primes_dac[j], primes_daclen[j], primes_daclen[j]);
  }
 
  // collect primes not used in the key ...
  int16_t unused[batch_stop[primes_batches - 1] + 1];
 
  int16_t u = 0;
  int16_t e = 0;
  int16_t w = 0;
  for (e = 0; e <= batch_stop[primes_batches - 1]; e++)
  {
#ifdef ENABLE_CT_TESTING
        VALGRIND_MAKE_MEM_DEFINED(&u, sizeof(int16_t));
        VALGRIND_MAKE_MEM_DEFINED(&e, sizeof(int16_t));
        VALGRIND_MAKE_MEM_DEFINED(&w, sizeof(int16_t));
#endif
 
    unused[u] = e;
 
    int64_t mov = -int64mask_equal((int64_t)e, (int64_t)priv->ells[w]);
 
    fp t1, t2;
    t1[0] = u;
    t2[0] = u + 1;
    fp_cmov(&t1, (const fp *)&t2, 1 - mov);
    u = t1[0];
 
    t1[0] = w;
    t2[0] = w + 1;
    fp_cmov(&t1, (const fp *)&t2, mov);
    w = t1[0];
  }
 
  // ... and remove them from our points
  int16_t tmp_b = 0;
  for (u = 0; u <= batch_stop[primes_batches - 1] - WOMBATKEYS; u++)
  {
    int16_t t = unused[u];
    if (t > batch_stop[tmp_b])
      tmp_b++;
 
    int64_t dac = lookup(t, primes_dac);
    int64_t daclen = lookup(t, primes_daclen);
 
    xMUL_dac(&Points[0], &A24, 0, &Points[0], dac, daclen, batch_maxdac[tmp_b]);
    xMUL_dac(&Points[1], &A24, 0, &Points[1], dac, daclen, batch_maxdac[tmp_b]);
  }
 
 
  proj ramifications[2 * WOMBATKEYS] = {0};
  int inner,
      block = 0, // current size of ramifications
      pos,       // index of the current small odd prime to be processed
      k = 0;     // strategy element
 
  int64_t moves = 0, // required for reaching an torsion-(l_pos) point
      xmul_counter[WOMBATKEYS] = {0},
          Plen = 0;
  (void)pos;
 
  int8_t swap = 0;
 
  proj_copy(&ramifications[0], (const proj *)&Points[0]); // point on E[\pi + 1]
  proj_copy(&ramifications[1], (const proj *)&Points[1]); // point on E[\pi - 1]
 
  int16_t current_batch = 0; //primes_batches - 1;
  int16_t current_batch_inner = batch_numkeys[current_batch];
 
  proj Points_[2 * WOMBATKEYS] = {0};
 
  // #pragma unroll WOMBATKEYS
  //int64_t tmp_cost = fpmul+fpsqr;
  for (int i = WOMBATKEYS - 1; i >= 0; i--)
  {
    if ((WOMBATKEYS - i - 1) > batch_keybounds_stop[current_batch])
    {
      current_batch++;
      current_batch_inner = batch_numkeys[current_batch];
    }
 
 
    uint16_t flip_index = WOMBATKEYS - i -1;
    uint16_t current_ell_index = priv->ells[flip_index];
    uint64_t current_ell = lookup(current_ell_index, primes);
    // 0 -> dummy, 1 -> + direction, 2 -> - direction
    int64_t direction = priv->directions[flip_index];
 
    uint64_t lowerend_ell = primes[batch_start[current_batch] + batch_numkeys[current_batch] - current_batch_inner];
    uint64_t upperend_ell = primes[batch_stop[current_batch] - current_batch_inner + 1];
 
 
    // conditional swap based on direction
    swap = -int64mask_equal(direction, (int64_t)2);
    proj_cswap(&ramifications[0+ 2 * block], &ramifications[1+ 2 * block], swap);
 
    tmp_b = primes_batches-1;
    while (moves < i)
    {
      block += 1;
 
      proj_copy(&ramifications[0 + 2 * block], (const proj *)&ramifications[0 + 2 * (block - 1)]); // point on E[\pi + 1]
      proj_copy(&ramifications[1 + 2 * block], (const proj *)&ramifications[1 + 2 * (block - 1)]); // point on E[\pi - 1]
 
      // #pragma unroll
      for (inner = moves; inner < (moves + strategy[k]); inner++)
      {
        pos = WOMBATKEYS - inner -1;
        while (pos < batch_keybounds_start[tmp_b])
          tmp_b--;
 
        int64_t dac = lookup(priv->ells[pos], primes_dac);
        int64_t daclen = lookup(priv->ells[pos], primes_daclen);
 
        if(moves + strategy[k] < i)
        {
          xMUL_dac(&ramifications[0 + 2 * block], &A24, 0, &ramifications[0 + 2 * block], dac, daclen, batch_maxdac[tmp_b]);
          xMUL_dac(&ramifications[1 + 2 * block], &A24, 0, &ramifications[1 + 2 * block], dac, daclen, batch_maxdac[tmp_b]);
        }
        else { // current block
          xMUL_dac(&ramifications[0 + 2 * block], &A24, 0, &ramifications[0 + 2 * block], dac, daclen, batch_maxdac[tmp_b]);
        }
      }
 
      xmul_counter[block] = strategy[k]; // the k-th element is used for next iteration on moves
      moves += strategy[k];              // moves is incremented
      k += 1;
    } 
 
    // how many points should be evaluated?
    Plen = 2 * block;
 
 
    proj Anew;
    proj_copy(&Anew, &A);
    for (int j = 0; j < Plen; j++)
    {
      // backup for the dummy case
      proj_copy(&Points_[j], &ramifications[j]);
    }
 
    xISOG_matryoshka(&Anew, Points_, Plen, &ramifications[0 + 2 * block], current_ell, lowerend_ell, upperend_ell);
 
 
    // copy back
    proj_cmov(&A, &Anew, -int64mask_nonzero(direction));
    xA24(&A24, &A);
 
 
    for (int j = 0; j < Plen; j++)
    {
      proj_cmov(&ramifications[j], &Points_[j], -int64mask_nonzero(direction));
 
      // in case of dummy, we still need to "remove" degree
      
      int64_t dac = lookup(current_ell_index, primes_dac);
      int64_t daclen = lookup(current_ell_index, primes_daclen);
 
      xMUL_dac(&ramifications[j], &A24, 0, &ramifications[j], dac, daclen, batch_maxdac[current_batch]);
    }
 
 
    // Configuring for the next iteration
    moves -= xmul_counter[block];
    xmul_counter[block] = 0;
    block -= 1;
    // swap back based on direction
    proj_cswap(&ramifications[0+ 2 * block], &ramifications[1+ 2 * block], swap);
 
    current_batch_inner--;
  }
 
#if defined(_M0_)
    fp_inv(A.z);
    fp_mul2(&A.x, (const fp *)&A.z);
    fp_copy(out->A, A.x);
#else
    isogeny_walks_3_fp(out->A, A, priv->radical_length, priv->radical_direction);
#endif
 
}

References public_key::A, batch_keybounds_start, batch_keybounds_stop, batch_maxdac, batch_numkeys, batch_start, batch_stop, private_key::directions, elligator_seeded, private_key::ells, fp_1, fp_cmov, fp_copy, fp_enc, fp_inv, i, isogeny_walks_3_fp(), j, primes, primes_dac, primes_daclen, private_key::radical_direction, private_key::radical_length, public_key::seed, strategy, swap(), xA24, xISOG_matryoshka, and xMUL_dac.

Here is the call graph for this function:

cofactor_multiples()

void cofactor_multiples	(	proj	P[],
		proj const	A,
		size_t	lower,
		size_t	upper
	)

Definition at line 77 of file validate.c.

{
    assert(lower < upper);
    if (upper - lower == 1)
        return;
 
    int i;
    size_t mid = lower + (upper - lower + 1) / 2;
 
    // proj_copy(P[mid], (const fp*)P[lower]);
    fp_copy(P[mid].x, P[lower].x);
    fp_copy(P[mid].z, P[lower].z);
 
    for (i = lower; i < (int)mid; i++)
        xMUL_dac(&P[mid], &A, 1, &P[mid], primes_dac[i], primes_daclen[i], primes_daclen[i]);
    // xmul(P[mid], i, (const fp*)P[mid], A);
 
    for (i = (int)mid; i < (int)upper; i++)
        xMUL_dac(&P[lower], &A, 1, &P[lower], primes_dac[i], primes_daclen[i], primes_daclen[i]);
    // xmul(P[lower], i, (const fp*)P[lower], A);
 
    cofactor_multiples(P, A, lower, mid);
    cofactor_multiples(P, A, mid, upper);
}

References assert(), cofactor_multiples, fp_copy, i, primes_dac, primes_daclen, and xMUL_dac.

Here is the call graph for this function:

csidh()

bool csidh	(	public_key *	out,
		public_key const *	in,
		private_key const *	priv
	)

Definition at line 394 of file ctidh.c.

{
  if (!validate(in))
  {
    fp_random(out->A);
    return false;
  }
  action(out, in, priv);
  return true;
}

References public_key::A, action, fp_random, i, and validate.

ctidh_private()

void ctidh_private

(

private_key *

priv

)

fulltorsion_points()

void fulltorsion_points	(	fp	u,
		fp const	a
	)

Definition at line 103 of file ctidh.c.

{
    proj Tp, Tm, Pp[batch_stop[primes_batches - 1] + 1], Pm[batch_stop[primes_batches - 1] + 1], A;
    int j;
 
    // Convert curve to projective Montgomery form (A' + 2C : 4C)
    fp_copy(A.x, a);
    fp_set1(A.z);
    fp_add(A.z, A.z, A.z); // 2C
    fp_add(A.x, A.x, A.z); // A' + 2C
    fp_add(A.z, A.z, A.z); // 4C
 
    fp_set0(u); // u <- 0
    uint8_t boolp = 0, boolm = 0;
 
    do
    {
 
#ifdef ENABLE_CT_TESTING
        VALGRIND_MAKE_MEM_DEFINED(&A, sizeof(proj));
        VALGRIND_MAKE_MEM_DEFINED(&boolp, sizeof(uint8_t));
        VALGRIND_MAKE_MEM_DEFINED(&boolm, sizeof(uint8_t));
        VALGRIND_MAKE_MEM_DEFINED(&Tp, sizeof(proj));
        VALGRIND_MAKE_MEM_DEFINED(Pp, sizeof(proj) * (batch_stop[primes_batches - 1] + 1 - batch_start[0]));
        VALGRIND_MAKE_MEM_DEFINED(Pm, sizeof(proj) * (batch_stop[primes_batches - 1] + 1 - batch_start[0]));
#endif
 
        fp_add(u, u, fp_1); // u <- u + 1 ... Recall, 1 must be in Montgomery domain
        elligator_seeded(&Tp, &Tm, &A, (const fp *)u);
 
        clearpublicprimes(&Tp, &A);
        clearpublicprimes(&Tm, &A);
        // clear ells replaced by radical 3-isogenies
        for (j = 0; j < batch_start[0]; j++)
        {
            xMUL_dac(&Tp, &A, 0, &Tp, primes_dac[j], primes_daclen[j], primes_daclen[j]);
            xMUL_dac(&Tm, &A, 0, &Tm, primes_dac[j], primes_daclen[j], primes_daclen[j]);
        }
        // clear ells not used in the keyspace
        for (j = batch_stop[primes_batches - 1] + 1; j < primes_num; j++)
        {
            xMUL_dac(&Tp, &A, 0, &Tp, primes_dac[j], primes_daclen[j], primes_daclen[j]);
            xMUL_dac(&Tm, &A, 0, &Tm, primes_dac[j], primes_daclen[j], primes_daclen[j]);
        }
 
        // Checking if Tp is an order (p+1)/(2^e)
        proj_copy(&Pp[0], &Tp);
        cofactor_multiples(Pp, A, 0, batch_stop[primes_batches - 1] + 1);
        boolp = 1;
        for (j = batch_start[0]; j < (int)(batch_stop[primes_batches - 1] + 1); j++)
            boolp &= (1 - fp_iszero(Pp[j].z));
 
        if (1 - boolp)
            continue;
 
        // ---> This can be removed for wd1 style
        // Checking if Tm is an order (p+1)/(2^e)
        proj_copy(&Pm[0], &Tm);
        cofactor_multiples(Pm, A, 0, batch_stop[primes_batches - 1] + 1);
 
        boolm = 1;
        for (j = batch_start[0]; j < (int)(batch_stop[primes_batches - 1] + 1); j++)
            boolm &= (1 - fp_iszero(Pm[j].z));
 
        if (1 - boolm)
            continue;
        // <---
    } while ((1 - boolp) | (1 - boolm));
 
    fp_dec(u, (uint64_t *const)u);
}

References a, batch_start, batch_stop, cofactor_multiples, elligator_seeded, fp_1, fp_add, fp_copy, fp_dec, i, j, primes_dac, primes_daclen, and xMUL_dac.

get_full_point()

uint64_t get_full_point	(	proj *	P,
		proj *	A
	)

validate()

bool validate

(

public_key const *

in

)

Definition at line 22 of file validate.c.

                                   {
// #if !defined(_M1_) && !defined(_M2_) && !defined(_M3_) && !defined(_M4_) && !defined(_M5_)
//     printf("\nNOT using radical 3-isogenies.\n\n");
// #else
//     printf("\nUsing 2^%ld radical 3-isogenies.\n\n", batch_start[0] - 1);
// #endif
    proj A, A24;
    fp_copy(A.x, in->A);
    fp_copy(A.z, fp_1);
    xA24(&A24, &A);
 
    proj Pp, Pm;
 
#ifdef ENABLE_CT_TESTING    
    memset(&Pp, 0, sizeof(proj));
    memset(&Pp.z, 0, sizeof(proj));
    VALGRIND_MAKE_MEM_DEFINED(&Pp.z, sizeof(fp));      
    VALGRIND_MAKE_MEM_DEFINED(&Pp, sizeof(proj)); 
    VALGRIND_MAKE_MEM_DEFINED(&A24, sizeof(proj));  
#endif 
 
    fp seed;
    fp_set(seed, in->seed);
    fp_enc(seed, seed);
    elligator_seeded(&Pp, &Pm, &A24, (const fp *)seed);
 
 
    for (int64_t j = 0; j < two_cofactor; j++)
    {
        xDBL(&Pp, &Pp, &A24, 0);
    }
    // clear ells replaced by radical 3-isogenies 
    for (int16_t j = 0; j < batch_start[0]; j++)
    {
      xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[j], primes_daclen[j], primes_daclen[j]);
    }
    // remove ells and check that we do not reach the point at infinity
    for(int i = primes_num-1; i > batch_start[0]; i--)
    {
        xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[i], primes_daclen[i], primes_daclen[i]);
        if(fp_iszero(Pp.z))
            return false;
    }
 
    // after removing the last ell, now we should have the point at infinity
    xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[batch_start[0]], primes_daclen[batch_start[0]], primes_daclen[batch_start[0]]);
    return fp_iszero(Pp.z);
}

References batch_start, elligator_seeded, fp_1, fp_copy, fp_enc, i, j, primes_dac, primes_daclen, xA24, xDBL, and xMUL_dac.

Variable Documentation

base

const public_key base

extern

Definition at line 29 of file ctidh.c.

{.A = {0}, .seed = ELLIGATOR_SEED}; /* A = 0 */

csidh_statsucceeded

long long csidh_statsucceeded[primes_batches]

extern

csidh_stattried

long long csidh_stattried[primes_batches]

extern