validate.c File Reference

#include <string.h>
#include <assert.h>
#include "../CTIDH/ctidh.h"
#include "primes.h"
#include "mont.h"
#include "elligator.h"

Include dependency graph for validate.c:

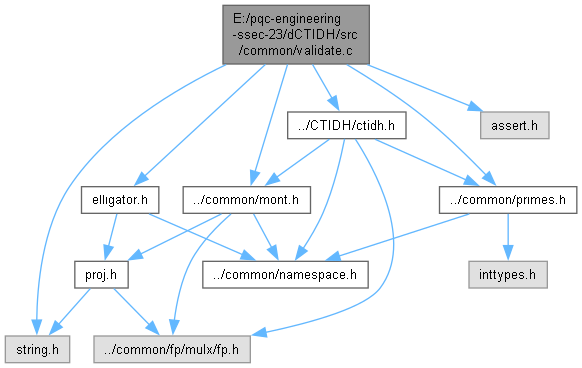
Go to the source code of this file.

Functions
bool	validate (public_key const *in)
void	cofactor_multiples (proj P[], proj const A, size_t lower, size_t upper)

Function Documentation

cofactor_multiples()

void cofactor_multiples	(	proj	P[],
		proj const	A,
		size_t	lower,
		size_t	upper
	)

Definition at line 77 of file validate.c.

{
    assert(lower < upper);
    if (upper - lower == 1)
        return;
 
    int i;
    size_t mid = lower + (upper - lower + 1) / 2;
 
    // proj_copy(P[mid], (const fp*)P[lower]);
    fp_copy(P[mid].x, P[lower].x);
    fp_copy(P[mid].z, P[lower].z);
 
    for (i = lower; i < (int)mid; i++)
        xMUL_dac(&P[mid], &A, 1, &P[mid], primes_dac[i], primes_daclen[i], primes_daclen[i]);
    // xmul(P[mid], i, (const fp*)P[mid], A);
 
    for (i = (int)mid; i < (int)upper; i++)
        xMUL_dac(&P[lower], &A, 1, &P[lower], primes_dac[i], primes_daclen[i], primes_daclen[i]);
    // xmul(P[lower], i, (const fp*)P[lower], A);
 
    cofactor_multiples(P, A, lower, mid);
    cofactor_multiples(P, A, mid, upper);
}

References assert(), cofactor_multiples, fp_copy, i, primes_dac, primes_daclen, and xMUL_dac.

Here is the call graph for this function:

validate()

bool validate

(

public_key const *

in

)

Definition at line 22 of file validate.c.

                                   {
// #if !defined(_M1_) && !defined(_M2_) && !defined(_M3_) && !defined(_M4_) && !defined(_M5_)
//     printf("\nNOT using radical 3-isogenies.\n\n");
// #else
//     printf("\nUsing 2^%ld radical 3-isogenies.\n\n", batch_start[0] - 1);
// #endif
    proj A, A24;
    fp_copy(A.x, in->A);
    fp_copy(A.z, fp_1);
    xA24(&A24, &A);
 
    proj Pp, Pm;
 
#ifdef ENABLE_CT_TESTING    
    memset(&Pp, 0, sizeof(proj));
    memset(&Pp.z, 0, sizeof(proj));
    VALGRIND_MAKE_MEM_DEFINED(&Pp.z, sizeof(fp));      
    VALGRIND_MAKE_MEM_DEFINED(&Pp, sizeof(proj)); 
    VALGRIND_MAKE_MEM_DEFINED(&A24, sizeof(proj));  
#endif 
 
    fp seed;
    fp_set(seed, in->seed);
    fp_enc(seed, seed);
    elligator_seeded(&Pp, &Pm, &A24, (const fp *)seed);
 
 
    for (int64_t j = 0; j < two_cofactor; j++)
    {
        xDBL(&Pp, &Pp, &A24, 0);
    }
    // clear ells replaced by radical 3-isogenies 
    for (int16_t j = 0; j < batch_start[0]; j++)
    {
      xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[j], primes_daclen[j], primes_daclen[j]);
    }
    // remove ells and check that we do not reach the point at infinity
    for(int i = primes_num-1; i > batch_start[0]; i--)
    {
        xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[i], primes_daclen[i], primes_daclen[i]);
        if(fp_iszero(Pp.z))
            return false;
    }
 
    // after removing the last ell, now we should have the point at infinity
    xMUL_dac(&Pp, &A24, 0, &Pp, primes_dac[batch_start[0]], primes_daclen[batch_start[0]], primes_daclen[batch_start[0]]);
    return fp_iszero(Pp.z);
}

References batch_start, elligator_seeded, fp_1, fp_copy, fp_enc, i, j, primes_dac, primes_daclen, xA24, xDBL, and xMUL_dac.