mont.c File Reference

#include <stdio.h>
#include <string.h>
#include <assert.h>
#include "steps.h"
#include "mont.h"
#include "../common/fp/mulx/fp.h"
#include "poly.h"
#include "int64mask.h"

Include dependency graph for mont.c:

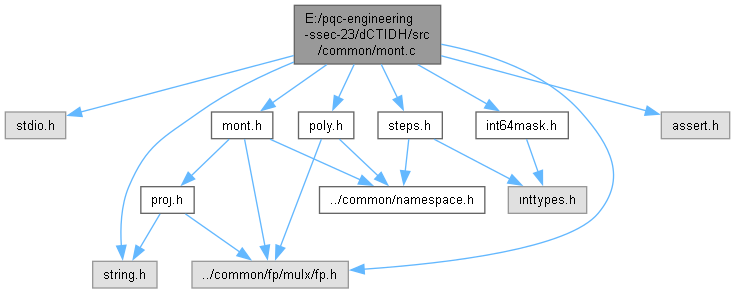
Go to the source code of this file.

Functions
void	xA24 (proj *A24, const proj *A)
void	xDBLADD (proj *R, proj *S, proj const *P, proj const *Q, proj const *PQ, proj const *A24, int Aaffine)
void	xDBL (proj *Q, proj const *P, const proj *A24, int Aaffine)
void	xADD (proj *S, proj const *P, proj const *Q, proj const *PQ)
void	xMUL_dac (proj *Q, proj const *A24, int Aaffine, proj const *P, int64_t dac, int64_t daclen, int64_t maxdaclen)
void	xMUL (proj *Q, proj const *A, int Aaffine, proj const *P, uintbig const *k, int64_t kbits)
void	xMUL_vartime (proj *Q, proj const *A, int Aaffine, proj const *P, uintbig const *k)
void	xISOG_matryoshka (proj *A, proj *P, int64_t Plen, proj const *K, int64_t k, int64_t klower, int64_t kupper)
void	xISOG (proj *A, proj *P, int64_t Plen, proj const *K, int64_t k)
void	xISOG_old (proj *A, proj *P, proj const *K, int64_t k)

Function Documentation

xA24()

void xA24	(	proj *	A24,
		const proj *	A
	)

Definition at line 20 of file mont.c.

{
    fp_double2(&A24->x, &A->z);
    fp_double2(&A24->z, (const fp *)&A24->x);
    fp_add2(&A24->x, &A->x);
}

References i.

xADD()

void xADD	(	proj *	S,
		proj const *	P,
		proj const *	Q,
		proj const *	PQ
	)

Definition at line 85 of file mont.c.

{
    fp a, b, c, d;
    fp_add3(&a, &P->x, &P->z);
    fp_sub3(&b, &P->x, &P->z);
    fp_add3(&c, &Q->x, &Q->z);
    fp_sub3(&d, &Q->x, &Q->z);
    fp_mul2(&a, (const fp *)&d);
    fp_mul2(&b, (const fp *)&c);
    fp_add3(&c, (const fp *)&a, (const fp *)&b);
    fp_sub3(&d, (const fp *)&a, (const fp *)&b);
    fp_sq1(&c);
    fp_sq1(&d);
    fp_mul3(&S->x, &PQ->z, (const fp *)&c);
    fp_mul3(&S->z, &PQ->x, (const fp *)&d);
}

References a, and i.

xDBL()

void xDBL	(	proj *	Q,
		proj const *	P,
		const proj *	A24,
		int	Aaffine
	)

Definition at line 78 of file mont.c.

{
    proj P2;
    x2(&P2, P);
    x2DBL(Q, &P2, A24, Aaffine);
}

References i.

xDBLADD()

void xDBLADD	(	proj *	R,
		proj *	S,
		proj const *	P,
		proj const *	Q,
		proj const *	PQ,
		proj const *	A24,
		int	Aaffine
	)

Definition at line 49 of file mont.c.

{
    fp tmp0, tmp1, tmp2;
 
    fp_add3(&tmp0, &P->x, &P->z);
    fp_sub3(&tmp1, &P->x, &P->z);
    fp_sq2(&R->x, (const fp *)&tmp0);
    fp_sub3(&tmp2, &Q->x, &Q->z);
    fp_add3(&S->x, &Q->x, &Q->z);
    fp_mul2(&tmp0, (const fp *)&tmp2);
    fp_sq2(&R->z, (const fp *)&tmp1);
    fp_mul2(&tmp1, (const fp *)&S->x);
    fp_sub3(&tmp2, (const fp *)&R->x, (const fp *)&R->z);
    if (Aaffine)
        fp_quadruple1(&R->z);
    else
        fp_mul2(&R->z, &A24->z);
    fp_mul2(&R->x, (const fp *)&R->z);
    fp_mul3(&S->x, &A24->x, (const fp *)&tmp2);
    fp_sub3(&S->z, (const fp *)&tmp0, (const fp *)&tmp1);
    fp_add2(&R->z, (const fp *)&S->x);
    fp_add3(&S->x, (const fp *)&tmp0, (const fp *)&tmp1);
    fp_mul2(&R->z, (const fp *)&tmp2);
    fp_sq1(&S->z);
    fp_sq1(&S->x);
    fp_mul2(&S->z, &PQ->x);
    fp_mul2(&S->x, &PQ->z);
}

References i.

xISOG()

void xISOG	(	proj *	A,
		proj *	P,
		int64_t	Plen,
		proj const *	K,
		int64_t	k
	)

Definition at line 789 of file mont.c.

{
    xISOG_matryoshka(A, P, Plen, K, k, k, k);
}

References i, and xISOG_matryoshka.

xISOG_matryoshka()

void xISOG_matryoshka	(	proj *	A,
		proj *	P,
		int64_t	Plen,
		proj const *	K,
		int64_t	k,
		int64_t	klower,
		int64_t	kupper
	)

Definition at line 429 of file mont.c.

{
    assert(3 <= klower);
    assert(klower & 1);
    assert(kupper & 1);
 
    int64_t sqrtvelu = 0;
    int64_t bs = 0;
    int64_t gs = 0;
 
    steps(&bs, &gs, klower);
    if (bs)
    {
        sqrtvelu = 1;
        assert(bs > 0);
        assert(gs > 0);
        assert(!(bs & 1));
    }
 
    fp tmp0, tmp1, tmp2, tmp3, tmp4;
 
    proj A24;
    proj Aed; // twisted Edwards curve coefficients
 
    // A -> (A : C)
    // Aed.z = 2C
    fp_double2(&Aed.z, (const fp *)&A->z);
 
    // Aed.x = A + 2C
    fp_add3(&Aed.x, (const fp *)&A->x, (const fp *)&Aed.z);
 
    // A24.x = A + 2C
    fp_copy(A24.x, Aed.x);
 
    // A24.z = 4C
    fp_double2(&A24.z, (const fp *)&Aed.z);
 
    // Aed.z = A - 2C
    fp_sub3(&Aed.z, (const fp *)&A->x, (const fp *)&Aed.z);
 
    proj M[kupper]; /* XXX: use less space */
#ifndef NDEBUG
    int Minit[kupper];
 
    for (int64_t s = 0; s < kupper; ++s)
        Minit[s] = 0;
 
    Minit[1] = 1;
#endif
    M[1] = *K;
    xDBL(&M[2], K, &A24, 0);
#ifndef NDEBUG
    Minit[2] = 1;
#endif
 
    if (sqrtvelu)
    {
        for (int64_t s = 3; s < kupper; ++s)
        {
            if (s & 1)
            {
                int64_t i = s / 2;
                assert(s == 2 * i + 1);
                if (i < bs)
                {
                    if (s == 3)
                    {
                        assert(Minit[1]);
                        assert(Minit[2]);
                        xADD(&M[s], &M[2], &M[1], &M[1]);
#ifndef NDEBUG
                        Minit[s] = 1;
#endif
                        continue;
                    }
                    assert(Minit[s - 2]);
                    assert(Minit[s - 4]);
                    assert(Minit[2]);
                    xADD(&M[s], &M[s - 2], &M[2], &M[s - 4]);
#ifndef NDEBUG
                    Minit[s] = 1;
#endif
                    continue;
                }
            }
            else
            {
                int64_t i = s / 2 - 1;
                assert(s == 2 * i + 2);
                if (i < (kupper - 1) / 2 - 2 * bs * gs)
                {
                    if (s == 4)
                    {
                        assert(Minit[2]);
                        xDBL(&M[s], &M[2], &A24, 0);
#ifndef NDEBUG
                        Minit[s] = 1;
#endif
                        continue;
                    }
                    assert(Minit[s - 2]);
                    assert(Minit[s - 4]);
                    assert(Minit[2]);
                    xADD(&M[s], &M[s - 2], &M[2], &M[s - 4]);
#ifndef NDEBUG
                    Minit[s] = 1;
#endif
                    continue;
                }
            }
 
            if (bs > 0)
            {
                if (s == 2 * bs)
                {
                    assert(Minit[bs - 1]);
                    assert(Minit[bs + 1]);
                    assert(Minit[2]);
                    xADD(&M[s], &M[bs + 1], &M[bs - 1], &M[2]);
#ifndef NDEBUG
                    Minit[s] = 1;
#endif
                    continue;
                }
                else if (s == 4 * bs)
                {
                    assert(Minit[2 * bs]);
                    xDBL(&M[s], &M[2 * bs], &A24, 0);
#ifndef NDEBUG
                    Minit[s] = 1;
#endif
                    continue;
                }
                else if (s == 6 * bs)
                {
                    assert(Minit[2 * bs]);
                    assert(Minit[4 * bs]);
                    xADD(&M[s], &M[4 * bs], &M[2 * bs], &M[2 * bs]);
#ifndef NDEBUG
                    Minit[s] = 1;
#endif
                    continue;
                }
                else if (s % (4 * bs) == 2 * bs)
                {
                    int64_t j = s / (4 * bs);
                    assert(s == 2 * bs * (2 * j + 1));
                    if (j < gs)
                    {
                        assert(Minit[s - 4 * bs]);
                        assert(Minit[s - 8 * bs]);
                        assert(Minit[4 * bs]);
                        xADD(&M[s], &M[s - 4 * bs], &M[4 * bs], &M[s - 8 * bs]);
#ifndef NDEBUG
                        Minit[s] = 1;
#endif
                        continue;
                    }
                }
            }
        }
    }
    else
    {
        for (int64_t i = 3; i <= (kupper - 1) / 2; ++i)
        {
#ifndef NDEBUG
            Minit[i] = 1;
#endif
            xADD(&M[i], &M[i - 1], K, &M[i - 2]);
        }
    }
 
    proj Abatch;
    fp_copy(Abatch.x, fp_1);
    fp_copy(Abatch.z, fp_1);
    int64_t fixPlen = 0;
    if(Plen>0) {
        fixPlen = Plen;
    } else {
        fixPlen = 1;
    }
    proj Qbatch[fixPlen];
    for (int64_t h = 0; h < Plen; ++h)
    {
        fp_copy(Qbatch[h].x, fp_1);
        fp_copy(Qbatch[h].z, fp_1);
    }
    fp Psum[fixPlen], Pdif[fixPlen];
    for (int64_t h = 0; h < Plen; ++h)
    {
        //precomputations
        // ( X + Z )
        fp_add3(&Psum[h], (const fp *)&P[h].x, (const fp *)&P[h].z);
        // ( X - Z )
        fp_sub3(&Pdif[h], (const fp *)&P[h].x, (const fp *)&P[h].z);
    }
 
    if (sqrtvelu)
    {
        int64_t TIlen = 2 * bs + poly_tree1size(bs);
        fp TI[TIlen];
 
        for (int64_t i = 0; i < bs; ++i)
        {
            assert(Minit[2 * i + 1]);
            fp_neg2(&TI[2 * i], (const fp *)&M[2 * i + 1].x);
            fp_copy(TI[2 * i + 1], M[2 * i + 1].z);
        }
 
        poly_tree1(TI + 2 * bs, (const fp *)TI, bs);
 
        fp Aprecomp[gs][8];
        fp T1[3 * gs];
        fp Tminus1[3 * gs];
 
        for (int64_t j = 0; j < gs; ++j)
        {
            assert(Minit[2 * bs * (2 * j + 1)]);
            biquad_precompute_curve(Aprecomp[j], &M[2 * bs * (2 * j + 1)], A);
            biquad_postcompute_curve(T1 + 3 * j, Tminus1 + 3 * j, (const fp *)Aprecomp[j]);
        }
        poly_multiprod2_selfreciprocal(T1, gs);
        poly_multiprod2_selfreciprocal(Tminus1, gs);
 
        int64_t precompsize = poly_multieval_precomputesize(bs, 2 * gs + 1);
        fp precomp[precompsize];
        poly_multieval_precompute(precomp, bs, 2 * gs + 1, (const fp *)TI, (const fp *)TI + 2 * bs);
 
        fp v[bs];
 
        poly_multieval_postcompute(v, bs, (const fp *)T1, 2 * gs + 1, (const fp *)TI, (const fp *)TI + 2 * bs, (const fp *)precomp);
        fp_copy(Abatch.x, v[0]);
        for (int64_t i = 1; i < bs; ++i)
            fp_mul2(&Abatch.x, (const fp *)&v[i]);
 
        poly_multieval_postcompute(v, bs, (const fp *)Tminus1, 2 * gs + 1, (const fp *)TI, (const fp *)TI + 2 * bs, (const fp *)precomp);
        fp_copy(Abatch.z, v[0]);
        for (int64_t i = 1; i < bs; ++i)
            fp_mul2(&Abatch.z, (const fp *)&v[i]);
 
        for (int64_t h = 0; h < Plen; ++h)
        {
            fp Pprecomp[6];
            biquad_precompute_point(Pprecomp, &P[h]);
 
            fp TP[3 * gs];
            for (int64_t j = 0; j < gs; ++j)
                biquad_postcompute_point(TP + 3 * j, (const fp *)Pprecomp, (const fp *)Aprecomp[j]);
            poly_multiprod2(TP, gs);
 
            fp TPinv[2 * gs + 1];
            for (int64_t j = 0; j < 2 * gs + 1; ++j)
                fp_copy(TPinv[j], TP[2 * gs - j]);
 
            poly_multieval_postcompute(v, bs, (const fp *)TP, 2 * gs + 1, (const fp *)TI, (const fp *)TI + 2 * bs, (const fp *)precomp);
            fp_copy(Qbatch[h].z, v[0]);
            for (int64_t i = 1; i < bs; ++i)
                fp_mul2(&Qbatch[h].z, (const fp *)&v[i]);
 
            poly_multieval_postcompute(v, bs, (const fp *)TPinv, 2 * gs + 1, (const fp *)TI, (const fp *)TI + 2 * bs, (const fp *)precomp);
            fp_copy(Qbatch[h].x, v[0]);
            for (int64_t i = 1; i < bs; ++i)
                fp_mul2(&Qbatch[h].x, (const fp *)&v[i]);
        }
 
        int64_t ignore = (k - 1) / 2 - 2 * bs * gs; /* skip i >= ignore */
        for (int64_t i = 0; i < (kupper - 1) / 2 - 2 * bs * gs; ++i)
        {
            int64_t want = -((i - ignore) >> 61); /* 61 to reduce risk of compiler doing something silly */
            assert(Minit[2 * i + 2]);
            fp_sub3(&tmp4, (const fp *)&M[2 * i + 2].x, (const fp *)&M[2 * i + 2].z);
            fp_add3(&tmp3, (const fp *)&M[2 * i + 2].x, (const fp *)&M[2 * i + 2].z);
            fp_mul3(&tmp2, (const fp *)&Abatch.x, (const fp *)&tmp4);
            fp_cmov_ctidh(&Abatch.x, (const fp *)&tmp2, want);
            fp_mul3(&tmp2, (const fp *)&Abatch.z, (const fp *)&tmp3);
            fp_cmov_ctidh(&Abatch.z, (const fp *)&tmp2, want);
            for (int64_t h = 0; h < Plen; ++h)
            {
                fp_mul3(&tmp1, (const fp *)&tmp4, (const fp *)&Psum[h]);
                fp_mul3(&tmp0, (const fp *)&tmp3, (const fp *)&Pdif[h]);
                fp_add3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
                fp_mul2(&tmp2, (const fp *)&Qbatch[h].x);
                fp_cmov_ctidh(&Qbatch[h].x, (const fp *)&tmp2, want);
                fp_sub3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
                fp_mul2(&tmp2, (const fp *)&Qbatch[h].z);
                fp_cmov_ctidh(&Qbatch[h].z, (const fp *)&tmp2, want);
            }
        }
    }
    else
    {
        // no sqrtvelu
        int64_t ignore = (k + 1) / 2; /* skip i >= ignore */
 
        assert(Minit[1]);
        fp_sub3(&tmp4, (const fp *)&M[1].x, (const fp *)&M[1].z);
        fp_add3(&tmp3, (const fp *)&M[1].x, (const fp *)&M[1].z);
        fp_copy(Abatch.x, tmp4);
        fp_copy(Abatch.z, tmp3);
 
        for (int64_t h = 0; h < Plen; ++h)
        {
            fp_mul3(&tmp1, (const fp *)&tmp4, (const fp *)&Psum[h]);
            fp_mul3(&tmp0, (const fp *)&tmp3, (const fp *)&Pdif[h]);
            fp_add3(&Qbatch[h].x, (const fp *)&tmp0, (const fp *)&tmp1);
            fp_sub3(&Qbatch[h].z, (const fp *)&tmp0, (const fp *)&tmp1);
        }
 
        for (int64_t i = 2; i <= (kupper - 1) / 2; ++i)
        {
            int64_t want = -((i - ignore) >> 61);
            // 2 < i < (k-1)/2
            assert(Minit[i]);
            fp_sub3(&tmp4, (const fp *)&M[i].x, (const fp *)&M[i].z);
            fp_add3(&tmp3, (const fp *)&M[i].x, (const fp *)&M[i].z);
            fp_mul3(&tmp2, (const fp *)&Abatch.x, (const fp *)&tmp4);
            fp_cmov_ctidh(&Abatch.x, (const fp *)&tmp2, want);
            fp_mul3(&tmp2, (const fp *)&Abatch.z, (const fp *)&tmp3);
            fp_cmov_ctidh(&Abatch.z, (const fp *)&tmp2, want);
            for (int64_t h = 0; h < Plen; ++h)
            {
                // point evaluation
                fp_mul3(&tmp1, (const fp *)&tmp4, (const fp *)&Psum[h]);
                fp_mul3(&tmp0, (const fp *)&tmp3, (const fp *)&Pdif[h]);
                fp_add3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
                fp_mul2(&tmp2, (const fp *)&Qbatch[h].x);
                fp_cmov_ctidh(&Qbatch[h].x, (const fp *)&tmp2, want);
                fp_sub3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
                fp_mul2(&tmp2, (const fp *)&Qbatch[h].z);
                fp_cmov_ctidh(&Qbatch[h].z, (const fp *)&tmp2, want);
            }
        }
    }
 
    for (int64_t h = 0; h < Plen; ++h)
    {
        // point evaluation
        // [∏( X − Z )( X i + Z i ) + ( X + Z )( X i − Z i )]^2
        fp_sq1(&Qbatch[h].x);
        fp_sq1(&Qbatch[h].z);
 
        // X' = X * Qbatch[h].x
        // X' = X * [∏( X − Z )( X i + Z i ) + ( X + Z )( X i − Z i )]^2
        fp_mul2(&P[h].x, (const fp *)&Qbatch[h].x);
        fp_mul2(&P[h].z, (const fp *)&Qbatch[h].z);
    }
 
    // Aed.x =  Aed.x^k * Abatch.z^8
    powpow8mod(&Aed.x, (const fp *)&Abatch.z, k, kupper);
    // Aed.z =  Aed.z^k * Abatch.x^8
    powpow8mod(&Aed.z, (const fp *)&Abatch.x, k, kupper);
 
    //compute Montgomery params
    // ( A' : C' ) = ( 2 ( a'_E + d'_E ) : a'_E − d'_E )
    fp_add3(&A->x, (const fp *)&Aed.x, (const fp *)&Aed.z);
    fp_sub3(&A->z, (const fp *)&Aed.x, (const fp *)&Aed.z);
    fp_double1(&A->x);
}

References assert(), fp_1, fp_copy, i, j, poly_multieval_postcompute, poly_multieval_precompute, poly_multieval_precomputesize, poly_multiprod2, poly_multiprod2_selfreciprocal, poly_tree1, poly_tree1size, steps, xADD, and xDBL.

Here is the call graph for this function:

xISOG_old()

void xISOG_old	(	proj *	A,
		proj *	P,
		proj const *	K,
		int64_t	k
	)

Definition at line 794 of file mont.c.

{
    assert(k >= 3);
    assert(k % 2 == 1);
 
    fp tmp0, tmp1, tmp2, Psum, Pdif;
    proj Q, Aed, prod;
 
    fp_add3(&Aed.z, (const fp *)&A->z, (const fp *)&A->z); //compute twisted Edwards curve coefficients
    fp_add3(&Aed.x, (const fp *)&A->x, (const fp *)&Aed.z);
    fp_sub3(&Aed.z, (const fp *)&A->x, (const fp *)&Aed.z);
 
    fp_add3(&Psum, (const fp *)&P->x, (const fp *)&P->z); //precomputations
    fp_sub3(&Pdif, (const fp *)&P->x, (const fp *)&P->z);
 
    fp_sub3(&prod.x, &K->x, &K->z);
    fp_add3(&prod.z, &K->x, &K->z);
 
    fp_mul3(&tmp1, (const fp *)&prod.x, (const fp *)&Psum);
    fp_mul3(&tmp0, (const fp *)&prod.z, (const fp *)&Pdif);
    fp_add3(&Q.x, (const fp *)&tmp0, (const fp *)&tmp1);
    fp_sub3(&Q.z, (const fp *)&tmp0, (const fp *)&tmp1);
 
    proj M[k];
    proj A24;
    xA24(&A24, A);
 
    M[0] = *K;
    xDBL(&M[1], K, &A24, 0);
    for (int64_t i = 2; i < k / 2; ++i)
    {
        xADD(&M[i], &M[(i - 1)], K, &M[(i - 2)]);
    }
 
    for (int64_t i = 1; i < k / 2; ++i)
    {
        fp_sub3(&tmp1, (const fp *)&M[i].x, (const fp *)&M[i].z);
        fp_add3(&tmp0, (const fp *)&M[i].x, (const fp *)&M[i].z);
        fp_mul2(&prod.x, (const fp *)&tmp1);
        fp_mul2(&prod.z, (const fp *)&tmp0);
        fp_mul2(&tmp1, (const fp *)&Psum);
        fp_mul2(&tmp0, (const fp *)&Pdif);
        fp_add3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
        fp_mul2(&Q.x, (const fp *)&tmp2);
        fp_sub3(&tmp2, (const fp *)&tmp0, (const fp *)&tmp1);
        fp_mul2(&Q.z, (const fp *)&tmp2);
    }
 
    // point evaluation
    fp_sq1(&Q.x);
    fp_sq1(&Q.z);
    fp_mul2(&P->x, (const fp *)&Q.x);
    fp_mul2(&P->z, (const fp *)&Q.z);
 
    //compute Aed.x^k, Aed.z^k
    exp_by_squaring_(&Aed.x, &Aed.z, k);
 
    //compute prod.x^8, prod.z^8
    fp_sq1(&prod.x);
    fp_sq1(&prod.x);
    fp_sq1(&prod.x);
    fp_sq1(&prod.z);
    fp_sq1(&prod.z);
    fp_sq1(&prod.z);
 
    //compute image curve parameters
    fp_mul2(&Aed.z, (const fp *)&prod.x);
    fp_mul2(&Aed.x, (const fp *)&prod.z);
 
    //compute Montgomery params
    fp_add3(&A->x, (const fp *)&Aed.x, (const fp *)&Aed.z);
    fp_sub3(&A->z, (const fp *)&Aed.x, (const fp *)&Aed.z);
    fp_add2(&A->x, (const fp *)&A->x);
}

References assert(), i, xA24, xADD, and xDBL.

Here is the call graph for this function:

xMUL()

void xMUL	(	proj *	Q,
		proj const *	A,
		int	Aaffine,
		proj const *	P,
		uintbig const *	k,
		int64_t	kbits
	)

Definition at line 156 of file mont.c.

{
    proj R = *P;
    proj A24;
    const proj Pcopy = *P; /* in case Q = P */
 
    fp_copy(Q->x, fp_1);
    fp_copy(Q->z, fp_0);
 
    xA24(&A24, A);
 
    int64_t prevbit = 0;
    while (kbits > 0)
    {
        --kbits;
 
        int64_t bit = uintbig_bit(k, kbits);
        int64_t bitxor = bit ^ prevbit;
 
        proj_cswap(Q, &R, bitxor);
 
        xDBLADD(Q, &R, Q, &R, &Pcopy, &A24, Aaffine);
 
        prevbit = bit;
    }
    proj_cswap(Q, &R, prevbit);
}

References fp_0, fp_1, fp_copy, i, uintbig_bit, xA24, and xDBLADD.

xMUL_dac()

void xMUL_dac	(	proj *	Q,
		proj const *	A24,
		int	Aaffine,
		proj const *	P,
		int64_t	dac,
		int64_t	daclen,
		int64_t	maxdaclen
	)

Definition at line 110 of file mont.c.

{
    proj Pinput = *P; // keeping copy since Q can overlap P
    proj P1 = Pinput;
    proj P2;
    xDBL(&P2, &P1, A24, Aaffine);
    proj P3;
    xADD(&P3, &P2, &P1, &P1);
    //   int64_t collision = fp_iszero(&Pinput.z);
    int64_t collision = fp_iszero(Pinput.z);
 
    for (;;)
    {
        int64_t want = 1 + int64mask_negative(daclen);
        proj_cmov(Q, &P3, want);
        if (maxdaclen <= 0)
            break;
 
        // invariant: P1+P2 = P3
        // odd dac: want to replace P1,P2,P3 with P1,P3,P1+P3
        // even dac: want to replace P1,P2,P3 with P2,P3,P2+P3
 
        proj_cswap(&P1, &P2, 1 - (dac & 1));
        // invariant: P1+P2 = P3
        // all cases: want to replace P1,P2,P3 with P1,P3,P1+P3
 
        // collision |= want&fp_iszero(&P2.z);
        collision |= want & fp_iszero(P2.z);
 
        proj next;
        xADD(&next, &P3, &P1, &P2);
        P2 = P3;
        P3 = next;
 
        maxdaclen -= 1;
        daclen -= 1;
        dac >>= 1;
    }
 
    proj_cmov(Q, &Pinput, collision);
    // in case of collision, input has the right order
}

References i, xADD, and xDBL.

xMUL_vartime()

void xMUL_vartime	(	proj *	Q,
		proj const *	A,
		int	Aaffine,
		proj const *	P,
		uintbig const *	k
	)

Definition at line 184 of file mont.c.

{
    int64_t kbits = UBITS;
    while (kbits && !uintbig_bit(k, kbits - 1))
        --kbits;
    xMUL(Q, A, Aaffine, P, k, kbits);
}

References i, UBITS, uintbig_bit, and xMUL.