random_walks3 Namespace Reference

Functions
	to_model (A, xP)
	isogeny3 (alpha, a1, a3)
	random_walk3 (a1, a3, path, setup)
	get_order3_points (A, setup)
	cgl_hash3 (message, setup, verbose=True)
	Charles-Goren-Lauter (CGL) Hash function concerning 3-isogeny walks.

Function Documentation

cgl_hash3()

cgl_hash3	(		message,
			setup,
			verbose = True
	)

Charles-Goren-Lauter (CGL) Hash function concerning 3-isogeny walks.

Definition at line 81 of file random_walks3.py.

def cgl_hash3(message, setup, verbose=True):
    p = setup['Fq'].characteristic()
 
    # SHAKE_256 algorithm from the hashlib module.
    s = hashlib.shake_256()
    s.update(message)
    length = int(floor((p.bit_length() / log(3, 2)) + 0.5))
    digest = s.hexdigest(p.bit_length() // 8)
    path = base_repr(int(digest, 16), base=3)[:length]
 
    if verbose:
        print('\nCGL Hash function over the 3-isogeny graph (CGLHash3)')
        print(f'Symmetric primitive:\t{s.name}')
        print(f'Message digest size:\t{len(digest) // 2} bytes')
        print(f'Random path of size:\t{len(path)} steps')
 
    P = get_order3_points(setup['A'], setup) # We determinstically take the first order-3 point
    for xP in P:
        assert(not (xP**2 * (3 * xP**2 + 4 * setup['A'] * xP + 6) - 1))
    
    # Recall, input and output of random_walk3() determines elliptic curves 
    # of the form y² + a₁xy + a₃y = x³ − 5a₁a₃x − (a₁³)a₃ − 7(a₃)²
    xP = P[0] # We determinstically take the first x-coordinate point
    a1, a3 = to_model(setup['A'], xP)
    a1, a3 = random_walk3(a1, a3, [ int(b) for b in path ], setup)
    return EllipticCurve(setup['Fq'], [a1, 0, a3, -5 * a1 * a3, -a1**3 * a3 - 7 * a3**2]).j_invariant()

References assert(), i, and random_walk3().

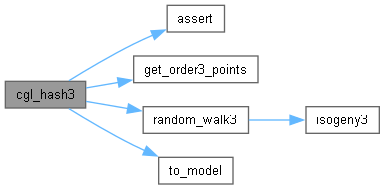
Here is the call graph for this function:

get_order3_points()

get_order3_points	(		A,
			setup
	)

Definition at line 42 of file random_walks3.py.

def get_order3_points(A, setup):
    Fq = setup['Fq']
    # Constants
    one_half = 1 / Fq(2)
    one_third = 1 / Fq(3)
    one_ninth = one_third**2
    one_by_27 = one_third * one_ninth
    
    A_times_one_third = A * one_third        #           M𝒸
    A_squared = A**2                         #       S 
    t = (Fq(3) - A_squared) * one_ninth      #           M𝒸 +  A
    r = 16 * (A_squared * A) * one_by_27     #    M    + M𝒸 + 4A
    s = 8 * A_times_one_third                #                3A
    u = r - s                                #                 A
    
    y = t + \
        one_third * \
            setup['curt'](-2 * A_squared + 8) #           M𝒸 + 3A + CURT
    
    r = 2 * y                                #                 A
    s = 6 * t                                #                3A
    
    s0 = setup['sqrt'](r - s)                #                 A +        SQRT
    i0 = 1 / s0                              # I
    v = -(r + s)                             #                2A
    s1 = setup['sqrt'](v + u * i0)           #    M         +  A +        SQRT
    s2 = setup['sqrt'](v - u * i0)           #    M         +  A +        SQRT
    
    z = []
    z.append((-s0 + s1) * one_half)          #           M𝒸 +  A  
    z.append((-s0 - s1) * one_half)          #           M𝒸 + 2A
    z.append((s0 + s2) * one_half)           #           M𝒸 +  A 
    z.append((s0 - s2) * one_half)           #           M𝒸 +  A 
    
    x = [zk-A_times_one_third for zk in z] #                  4A
    return x                    # Total cost: I + 3M + S + 8M𝒸 + 30A + CURT + 3SQRT
    
    

References i.

isogeny3()

isogeny3	(		alpha,
			a1,
			a3
	)

Definition at line 20 of file random_walks3.py.

def isogeny3(alpha, a1, a3):
    _a1 = -6 * alpha + a1
    _a3 = 3 * a1 * alpha**2 - a1**2 * alpha + 9 * a3
    return _a1, _a3
 
 

random_walk3()

random_walk3	(		a1,
			a3,
			path,
			setup
	)

Definition at line 27 of file random_walks3.py.

def random_walk3(a1, a3, path, setup):
    # This function assumes the input and output determines elliptic
    # curves of form y² + a₁xy + a₃y = x³ − 5a₁a₃x − (a₁³)a₃ − 7(a₃)²
    Fq = setup['Fq']
    a1_ = deepcopy(a1)
    a3_ = deepcopy(a3)
    for k in range(0, len(path), 1):
        alpha = [Fq(1), setup['ζ₃'], setup['ζ₃']**2][path[k]] * setup['curt'](-a3_)
        assert alpha**3 == -a3_
        a1_, a3_ = isogeny3(alpha, a1_, a3_)
 
    return a1_, a3_
 
 

References i.

Referenced by cgl_hash3().

Here is the caller graph for this function:

to_model()

to_model	(		A,
			xP
	)

Definition at line 13 of file random_walks3.py.

def to_model(A, xP):
    a1 = (3 * xP**2 + 2 * A * xP + 1)
    a3 = 2 * (xP**3 + A * xP**2 + xP)**2
    return a1, a3